Positions and coordinates
A position or point is a single location in 2D or 3D space, which may or may not be occupied by a physical object. Positions exist before we measure or describe them in any way, but to do calculations we need to introduce coordinates for positions.
A coordinate chart is a map that takes a position in space and tells us what its coordinates are. Coordinates serve to label positions. For example, the coordinates “5th Ave. and 42nd St.” label the intersection next to the New York Public Library in the street map coordinate chart. The coordinates of a position are a list of scalars that act as a label for the position, such as $x = 42$, $y = 5$ for this position in New York.
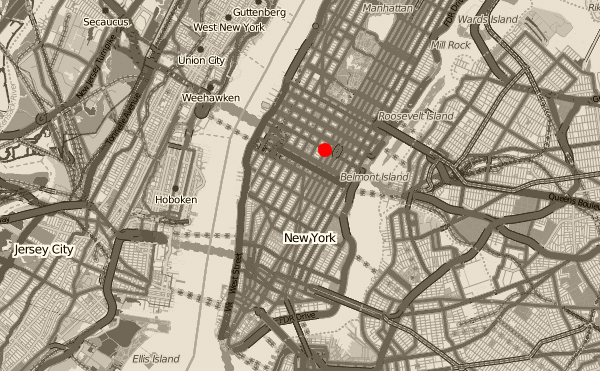
The location of the New York Public Library shown on a street map of Manhattan. Image credit: OpenStreet Browser (ODbL).
It is common to have several different coordinate charts in use for the same positions in space. For example, 40° 45′ 12.46″ N, 73° 58′ 51.16″ W are also coordinates for this same intersection, but this time in the latitude/longitude coordinate chart, which we could write as the pair of scalars $\lambda = -73.980878°$, $\phi = 40.753461°$.
We can also think of a coordinate chart as mapping a list of coordinates to a particular point, which is how we often illustrate a coordinate chart graphically. For example, if we know a latitude and longitude then we can locate the corresponding point on the Earth. The origin of a coordinate chart is the point with all zero coordinates. Different coordinate charts may share an origin, or they may have different origins.
When we describe a coordinate chart mathematically, we do so by relating it to another coordinate chart (typically Cartesian).
Cartesian Coordinates
Cartesian coordinates (also known as rectangular coordinates) are the regular $x,y$ or $x,y,z$ coordinates in 2D and 3D, with perpendicular straight-line axes.
| coordinate | name | range | definition |
|---|---|---|---|
| $x$ | horizontal | $-\infty \lt x \lt \infty$ | horizontal distance from the $y$-axis |
| $y$ | vertical | $-\infty \lt y \lt \infty$ | vertical distance from the $x$-axis |
In 3D the $x$,$y$,$z$ axes are oriented in right-handed order, so that fingers curling from $x$ to $y$ means the thumb points in the $z$ direction.
Cartesian coordinate system, showing the origin $O$ and three positions with their coordinates.
When writing coordinates we can either list the coordinate values explicitly, like $x = 2$, $y = 1$, or we can just write the numbers in an ordered list, like $(2, 1)$.
Writing them as a list assumes that we know which coordinate system we are using, and which order the coordinates are in. We will typically write the coordinate values explicitly to avoid confusion. This also applies to vector components.
While the idea of $x,y$ coordinates specifying positions might seem obvious, the use of algebraic quantities to define geometry in this way was a major discovery of René Descartes and a key event in the scientific revolution. Descartes was also instrumental in establishing the philosophical groundwork of The Enlightenment, and we owe to him the famous phrase “Cogito ergo sum”.
Polar Coordinates
Polar coordinates are an alternative 2D coordinate system that are useful for rotating or circular motion.
| coordinate | name | range | definition |
|---|---|---|---|
| $r$ | radius | $0 \le r \lt \infty$ | distance from the origin $O$ |
| $\theta$ | angle | $-\pi \lt \theta \le \pi$ | angle from the $x$-axis in the $x$–$y$ plane |
The two common extensions of polar coordinates to 3D are cylindrical coordinates and spherical coordinates.
Polar coordinate system, showing the origin $O$ and three positions with their coordinates.
To define polar coordinates, we relate them to another known coordinate system, typically Cartesian coordinates as follows, where we use the atan2 function.
Conversion between polar and Cartesian coordinates
\[\begin{aligned} x &= r \cos\theta & r &= \sqrt{x^2 + y^2} \\ y &= r \sin\theta & \theta &= \operatorname{atan2}(y, x) \end{aligned}\]
Angles can be measured in many different units. While radians are the most mathematically elegant unit, their use dates only from Roger Cotes in the 18th century. Degrees are a much older unit, dating back to the sexagesimal number system of the ancient Babylonians, and are convenient for celestial calculations because there are approximately 360 days in one year. Other units include grads (100 grads in a right angle) and mils (various definitions, all approximately equal to a milliradian).
When solving for $\theta$ in terms of $x$ and $y$ we know that $\tan\theta = y / x$. However, this does not necessary mean that $\theta = \tan^{-1}(y / x)$, because $\tan$ is not a one-to-one function. For example, $\tan^{-1}(1/1)$ is the same as $\tan^{-1}(-1/-1)$. We thus need to take $\theta = \tan^{-1}(y/x) + \pi$ if the point is in quadrants II or III.
An alternative is to use the atan2 function, which takes $x$ and $y$ as separate arguments and correctly handles the conversion to $\theta$ in any quadrant. This function is available in all common programming languages, including C, MATLAB, Python, and others.
Scientific calculators typically have special commands to convert to/from polar and Cartesian coordinates, which also automatically correctly handle the different quadrants.
Coordinates and units
When using coordinates to describe the location of physical positions in the real world, we must always have appropriate units of length for the coordinates. For example, the following coordinates all specify the same position: \[\begin{aligned} x &= 2{\rm\ m} & x &= 6.56{\rm\ ft} & r &= 6.32{\rm\ m} & r &= 249{\rm\ in} \\ y &= -6{\rm\ m} & y &= -6 \times 10^6{\rm\ \mu m} & \theta &= 1.25{\rm\ rad} & \theta &= 71.6^\circ. \end{aligned}\]
It is important to distinguish between units and dimensions. The base dimensions include mass (M), length (L), and time (T), and can be combined to produce dimensions such as L/T or L T$^{-1}$ for velocity. Each physical quantity such as velocity has just one set of dimensions, and there is no choice in this.
Units are particular ways of measuring dimensional quantities, and include the SI units kilogram (kg), meter (m), and second (s), as well as the customary U.S. units pound (lb) and foot (ft). A given physical quantity can be written in terms of many different units, although all of these must conform to the dimensions of the quantity. For example, velocity has dimension L/T and so it can be written in terms of the units m/s, ft/s, km/h, or many other choices.
Angles are an example of a dimensionless quantity (having dimension 1), but they still have units, typically either radians (rad) or degrees (°).
The SI unit system is the definitive system of measurement used in science and engineering. Other systems, such as U.S. customary units are defined in terms of SI units, so that an inch is defined to be exactly 2.54 cm, for example.
The National Institute of Standards and Technology (NIST) maintains an excellent reference guide to SI units, including precise rules and style conventions for writing units in scientific and engineering work.
Moving points
If we have a point that moves around in space, then its coordinates will change with time. It is also possible for the coordinate chart itself to be moving in time, so that even if a point remains stationary in space, its coordinates might be changing.
Movement: point coordinates
A point $P$ and two coordinate charts: Cartesian coordinates with origin $O_1$ and polar coordinates with origin $O_2$. The coordinates will change as either the point $P$ moves or as the coordinate charts move.